Как рассчитывается величина приведенного момента

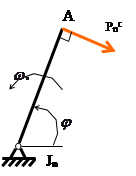
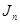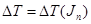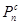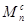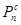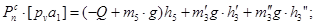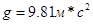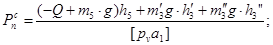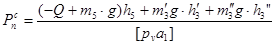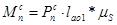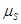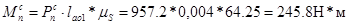Определение приведенного момента сопротивления рабочей машины

4. Определение приведенного момента сопротивления рабочей машины.

При подъеме груза величина момента сопротивления, когда поток энергии идет от двигателя к рабочей машине, находится из уравнения:

где i – передаточное отношение (i = 25.22);

М_рм = момент сопротивления на валу рабочей машины

где Q+Q₀ – вес груза с крюком (кг) (Q+Q₀ = 5775 кг)

D_б – диаметр барабана (D_б = 0.4 м)

m – число полиспастов (m = 2)

 — кпд электропривода ( = 0.84)

5. Определение времени пуска и торможения привода.

Время пуска и торможения двигателя определяется по формулам:

где GD 2 – маховый момент системы электропривода (GD 2 = 12.84 );

n_дв – частота вращения двигателя (n_дв = 723 );

М_j – динамический момент электропривода

Знак плюс у момента Мg берётся в том случае, когда двигатель работает в двигательном режиме, а знак минус – при тормозном режиме.

Знак плюс у момента сопротивления выбирается в том случае, когда рабочая машина по-

могает движению системы (при опускании груза), а знак минус, если рабочая машина мешает движению системы.

Величина момента двигателя находится из уравнения:

где  — коэффициент, зависящий от типа двигателя и условия пуска.

Для двигателя постоянного тока и асинхронных двигателей с фазным ротором

Для данного двигателя  = 1.6.

где М_н – номинальный момент двигателя

Р_н – номинальная мощность двигателя (Р_н = 22 кВт);

n_дв – частота вращения двигателя (n_дв = 723)

Мj₁ = Мg – М_с = 47.47 – 32.45 = 15.02

Мj₂ = — Мg – М_с = — 47.47 – 32.45 = — 79.92

В дальнейших расчётах знак минус, стоящий у времени торможения, не учитывается.

Определение пути, пройденного рабочим органом за время пуска и

Путь, пройденный рабочим органом за время пуска и торможения, вычисляется по формулам:

1.3 Определение приведенного момента движущих сил

Приведение моментов сил осуществляется на основе метода приведения сил. В основу метода положено равенство элементарных работ реальных сил, действующих в механизме и суммарного приведенного момента всех сил.

Момент приведенный от движущих сил определяется из соотношения:

, где V_qb – передаточная функция.

Для определения передаточной функции строим планы возможных скоростей. Зададимся отрезком изображающим скорость точки А кривошипа равным 50 мм. Скорости точек В и С находим из векторных уравнений:

Значения передаточных функций и приведенного момента движущих сил приведены в таблицах 1.2, 1.3, 1.4:

Передаточные функции цилиндра компрессора и двс в приложении.

1.4 Определение приведенного момента сил сопротивления

Момент приведенный от сил сопротивления определяется из соотношения:

, где V_qc – передаточная функция.

Значения передаточных функций и приведенного момента сил сопротивления приведены в таблицах 1.2, 1.3, 1,4.

1.5 Определение суммарного приведенного момента

Суммарный приведенный момент определяется как сумма приведенного момента движущих сил и приведенного момента сил сопротивления:

Значения суммарного приведенного момента приведены в таблицах 1.2, 1.3, 1.4.

Суммарный приведенный момент см в приложении.

Вычисляем масштаб графика суммарного приведенного момента и масштаб этого графика по оси абсцисс:

Моментами, от действия сил тяжести звеньев пренебрегаем, так как их величина очень незначительна – менее 5 % от максимального суммарного приведенного момента.

1.6 Построение графика суммарной работы

Построение графика работы движущих сил производится путем графического интегрирования графика приведенного момента движущих сил.

Отрезок интегрирования ОК выбираем равным 60 мм.

Построение графика работы сил сопротивления производится путем графического интегрирования графика приведенного момента сил сопротивления.

Отрезок интегрирования ОК выбираем равным 60 мм.

Режим установившийся следовательно работа движущих сил равна работе сил сопротивления. Полученный при графическом интегрировании график работы движущих сил необходимо растянуть по оси ординат в

Построение графика суммарной работы производится путем графического сложения графиков работы движущих сил и сил сопротивления

Масштаб графика работы определим по соотношению:

1.7 Определение приведенного момента инерции II группы звеньев механизма двс

Приведение моментов инерции осуществили на основе метода приведения масс. В основу метода положено равенство кинетической энергии всех звеньев механизма и звена динамической модели. В этом случае закон движения последнего будет таким же, как и закон движения начального звена реального механизма.

Суммарный приведенный момент инерции всего механизма равен сумме приведенных моментов инерции всех его звеньев. Суммарный приведенный момент инерции второй группы звеньев (поршней 3 и 5 и шатунов 2 и 4) рассчитывается по формуле:

,

где I_3П пр — приведенный момент инерции поршня ДВС при его поступательном движении;

где I_5П пр — приведенный момент инерции поршня компрессора при его поступательном движении;

I_2П пр — приведенный момент инерции шатуна 2 при его поступательном движении;

I_4П пр — приведенный момент инерции шатуна 4 при его поступательном движении;

I_2Вр пр — приведенный момент инерции шатуна 2 при его вращательном движении;

I_4Вр пр — приведенный момент инерции шатуна 4 при его вращательном движении.

Приведенные моменты инерции элементов при поступательном движении рассчитываются по формулам:

, где

V_i — скорость поступательного движения звена [м/с];

₁ — угловая скорость кривошипа 1 [рад/с];

m_i — масса звена [кг].

Приведенные моменты инерции шатунов 2 и 4 при их вращательном движении рассчитываются по формуле:

, где

_i — угловая скорость звена [рад/с];

I_is -момент инерции звена относительно оси, проходящей через центр тяжести [кгм 2 ].

Суммарный приведенный момент инерции всего механизма = + , где — приведенный момент инерции первой группы звеньев. Результаты расчетов представлены отдельно в виде группы таблиц и графиков

Вычислим масштаб графика суммарного приведенного момента инерции II группы звеньев:

Определение приведенных сил и моментов сопротивления.

Под машинным агрегатом понимается совокупность механизмов двигателя, передаточных механизмов и механизмов рабочей машины.

Для определения приведенной силы сопротивления необходимо весь машинный агрегат заменить динамической моделью:

Рис. 1.7.1. Схема привода машинного агрегата

Рис. 1.7.2. Динамическая модель

Приведенная сила (P_n c ) – сила, условно приложенная к точке приведения, работа которой на нее элементарном перемещении равна сумме работ всех сил и пар сил, действующих на звенья механизма.

Приведенный момент инерции – это есть момент инерции вращающегося тела вместе со звеном АО₁ тела, кинетическая энергия которого в каждом рассматриваемом положении механизма равна сумме кинетических энергий всех его звеньев.

Приведенные моменты инерции />машинного агрегата могут быть или постоянными, или зависящими от положения начального звена. В данном случае (долбежный станок) инерции />зависит от угла поворота j начального звена.

В большинстве технических задач приведенный момент движущих сил и приведенный момент сил сопротивления задаются в виде графиков. В виде графика также задается и приведенный момент инерции. Поэтому решение уравнений движений механизма ведется графочисленными методами. При графочисленном решении уравнений движения удобно применить уравнение кинетической энергии. Для того использовать диаграмму , устанавливающей связь между кинетической энергией Т и приведенным моментом инерции .

1.8. Определение приведенной силы сопротивления приведенного момента сопротивления .

Для определения приведенной силы используют рычаг Костера т.е. на повернутом плане скоростей параллельно самим себе переносим все силы, действующие на звенья механизма.

Приведенная сила – это сила, приложенная к кривошипу и ему перпендикулярна, причем работа приведенной силы, умноженная на ее элементарное перемещение равна сумме работ всех сил и пар сил, действующих на звенья.

Определение приведенной силы сопротивления (пример для 5-го положения механизма).

(1.8.1)

где — ускорение свободного падения.

откуда находим

(1.8.2.)

где — масштабный коэффициент механизма.

Аналогично определяются и для 11 других положений механизма:

Таблица 1.8.1. приведенные силы сопротивления и приведенные моменты сопротивления .

Определение приведенных моментов сил

Приведенный момент движущих сил М , приложенный к звену приведения, определяется из условия равенства мгновенных мощностей, т. е. Мощность, развиваемая М , равна сумме мощностей, развиваемых силами и моментами сил, действующими на звенья машинного агрегата. Так, для кривошипно-ползунного механизма с вертикальным движением ползуна, если в качестве звена приведения принимается вал кривошипа, приведенный момент движущих сил и сил тяжести (Н×м) равен:

(Силы берутся по модулю, знак перед угловой скоростью w учитывает, что вращения кривошипа направлено против часовой стрелки)

После подстановки числовых данных получим:

Приведенный момент сил сопротивления M в дальнейшем предполагается постоянным по величине, т. е. M = const, и находится из условия равенства работ движущих сил и сил сопротивления за цикл установившегося движения.

По распечатке ТММ1 строим диаграмму M = M (j) приведенных моментов движущих сил и сил тяжести в функции угла поворота j звена приведения. Принимаем масштаб моментов равным m_M =52.697 Н×м/мм, а масштаб углов поворота звена приведения: m_j =0.0261 рад/мм

где y_A – отрезок в десятом положении на диаграмме работ движущих сил, мм.

Полагая, что приведенный момент М сил сопротивления имеет постоянную величину во всех положениях звена приведения, строим диаграмму A _с= A _с(j), соединив начальную и конечную точки диаграммы A _д= A _д(j).

где y_A – отрезок в десятом положении на диаграмме работ сопротивления, мм.

Продифференцировав диаграмму A _с= A _с(j) по j, получим прямую, параллельную оси абсцисс, которая является диаграммой моментов сил сопротивления M = M (j).

где y_M – отрезок в десятом положении на диаграмме приведенного момента сопротивления, мм.